Python-Control Classes

The State Space Module

stateSpace.py

State space representation and functions.

This file contains the StateSpace class, which is used to represent linear systems in state space. This is the primary representation for the python-control library.

Routines in this module:

StateSpace.__init__ StateSpace._remove_useless_states StateSpace.copy StateSpace.__str__ StateSpace.__neg__ StateSpace.__add__ StateSpace.__radd__ StateSpace.__sub__ StateSpace.__rsub__ StateSpace.__mul__ StateSpace.__rmul__ StateSpace.__div__ StateSpace.__rdiv__ StateSpace.evalfr StateSpace.freqresp StateSpace.pole StateSpace.zero StateSpace.feedback StateSpace.returnScipySignalLti _convertToStateSpace _rss_generate

class statesp.StateSpace(*args)

The StateSpace class represents state space instances and functions.

The StateSpace class is used throughout the python-control library to represent systems in state space form. This class is derived from the Lti base class.

The main data members are the A, B, C, and D matrices. The class also keeps track of the number of states (i.e., the size of A).

Methods

evalfr(omega)

Evaluate a SS system’s transfer function at a single frequency.

self.evalfr(omega) returns the value of the transfer function matrix with input value s = i * omega.

feedback(other, sign=-1)

Feedback interconnection between two LTI systems.

freqresp(omega)

Evaluate the system’s transfer func. at a list of ang. frequencies.

mag, phase, omega = self.freqresp(omega)

reports the value of the magnitude, phase, and angular frequency of the system’s transfer function matrix evaluated at s = i * omega, where omega is a list of angular frequencies, and is a sorted version of the input omega.

pole()

Compute the poles of a state space system.

returnScipySignalLti()

Return a list of a list of scipy.signal.lti objects.

For instance,

>>> out = ssobject.returnScipySignalLti()
>>> out[3][5]

is a signal.scipy.lti object corresponding to the transfer function from the 6th input to the 4th output.

zero()

Compute the zeros of a state space system.

statesp.rand(d0, d1, ..., dn)

Random values in a given shape.

Create an array of the given shape and propagate it with random samples from a uniform distribution over [0, 1).

Parameters :

d0, d1, ..., dn : int

Shape of the output.

Returns :

out : ndarray, shape (d0, d1, ..., dn)

Random values.

See also

random

Notes

This is a convenience function. If you want an interface that takes a shape-tuple as the first argument, refer to random.

Examples

>>> np.random.rand(3,2)
array([[ 0.14022471,  0.96360618],  #random
       [ 0.37601032,  0.25528411],  #random
       [ 0.49313049,  0.94909878]]) #random

statesp.randn([d1, ..., dn])

Return a sample (or samples) from the “standard normal” distribution.

If positive, int_like or int-convertible arguments are provided, randn generates an array of shape (d1, ..., dn), filled with random floats sampled from a univariate “normal” (Gaussian) distribution of mean 0 and variance 1 (if any of the 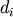are floats, they are first converted to integers by truncation). A single float randomly sampled from the distribution is returned if no argument is provided.

This is a convenience function. If you want an interface that takes a tuple as the first argument, use numpy.random.standard_normal instead.

Parameters :

d1, ..., dn : n ints, optional

The dimensions of the returned array, should be all positive.

Returns :

Z : ndarray or float

A (d1, ..., dn)-shaped array of floating-point samples from the standard normal distribution, or a single such float if no parameters were supplied.

See also

random.standard_normal

Similar, but takes a tuple as its argument.

Notes

For random samples from 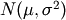, use:

sigma * np.random.randn(...) + mu

Examples

>>> np.random.randn()
2.1923875335537315 #random

Two-by-four array of samples from N(3, 6.25):

>>> 2.5 * np.random.randn(2, 4) + 3
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],  #random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]]) #random

The Transfer Function Module

xferfcn.py

Transfer function representation and functions.

This file contains the TransferFunction class and also functions that operate on transfer functions. This is the primary representation for the python-control library.

Routines in this module:

TransferFunction.__init__ TransferFunction._truncatecoeff TransferFunction.copy TransferFunction.__str__ TransferFunction.__neg__ TransferFunction.__add__ TransferFunction.__radd__ TransferFunction.__sub__ TransferFunction.__rsub__ TransferFunction.__mul__ TransferFunction.__rmul__ TransferFunction.__div__ TransferFunction.__rdiv__ TransferFunction.evalfr TransferFunction.freqresp TransferFunction.pole TransferFunction.zero TransferFunction.feedback TransferFunction.returnScipySignalLti TransferFunction._common_den _tfpolyToString _addSISO _convertToTransferFunction

class xferfcn.TransferFunction(*args)

The TransferFunction class represents TF instances and functions.

The TransferFunction class is derived from the Lti parent class. It is used throught the python-control library to represent systems in transfer function form.

The main data members are ‘num’ and ‘den’, which are 2-D lists of arrays containing MIMO numerator and denominator coefficients. For example,

>>> num[2][5] = numpy.array([1., 4., 8.])

means that the numerator of the transfer function from the 6th input to the 3rd output is set to s^2 + 4s + 8.

Methods

evalfr(omega)

Evaluate a transfer function at a single angular frequency.

self.evalfr(omega) returns the value of the transfer function matrix with input value s = i * omega.

feedback(other, sign=-1)

Feedback interconnection between two LTI objects.

freqresp(omega)

Evaluate a transfer function at a list of angular frequencies.

mag, phase, omega = self.freqresp(omega)

reports the value of the magnitude, phase, and angular frequency of the transfer function matrix evaluated at s = i * omega, where omega is a list of angular frequencies, and is a sorted version of the input omega.

pole()

Compute the poles of a transfer function.

returnScipySignalLti()

Return a list of a list of scipy.signal.lti objects.

For instance,

>>> out = tfobject.returnScipySignalLti()
>>> out[3][5]

is a signal.scipy.lti object corresponding to the transfer function from the 6th input to the 4th output.

zero()

Compute the zeros of a transfer function.