Creating System Models¶

Python-control provides a number of methods for creating LTI control systems.

`ss()`	create state-space (SS) models
`tf()`	create transfer function (TF) models

System creation¶

control.StateSpace()¶

The StateSpace class represents state space instances and functions.

The StateSpace class is used throughout the python-control library to represent systems in state space form. This class is derived from the Lti base class.

The main data members are the A, B, C, and D matrices. The class also keeps track of the number of states (i.e., the size of A).

Discrete time state space system are implemented by using the ‘dt’ class variable and setting it to the sampling period. If ‘dt’ is not None, then it must match whenever two state space systems are combined. Setting dt = 0 specifies a continuous system, while leaving dt = None means the system timebase is not specified. If ‘dt’ is set to True, the system will be treated as a discrete time system with unspecified sampling time.

control.ss(*args)¶

Create a state space system.

The function accepts either 1 or 4 parameters:

ss(sys)

Convert a linear system into space system form. Always creates a new system, even if sys is already a StateSpace object.

ss(A, B, C, D)

Create a state space system from the matrices of its state and output equations:

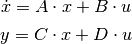
$\dot x = A \cdot x + B \cdot u y = C \cdot x + D \cdot u$

The matrices can be given as array like data types or strings. Everything that the constructor of numpy.matrix accepts is permissible here too.

Parameters:

sys: Lti (StateSpace or TransferFunction)

A linear system

A: array_like or string

System matrix

B: array_like or string

Control matrix

C: array_like or string

Output matrix

D: array_like or string

Feed forward matrix

Returns:

out: StateSpace

The new linear system

Raises:

ValueError

if matrix sizes are not self-consistent

See also

tf, ss2tf, tf2ss

Examples

>>> # Create a StateSpace object from four "matrices".
>>> sys1 = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.") 

>>> # Convert a TransferFunction to a StateSpace object.
>>> sys_tf = tf([2.], [1., 3])
>>> sys2 = ss(sys_tf) 

control.TransferFunction()¶

The TransferFunction class represents TF instances and functions.

The TransferFunction class is derived from the Lti parent class. It is used throught the python-control library to represent systems in transfer function form.

The main data members are ‘num’ and ‘den’, which are 2-D lists of arrays containing MIMO numerator and denominator coefficients. For example,

>>> num[2][5] = numpy.array([1., 4., 8.])

means that the numerator of the transfer function from the 6th input to the 3rd output is set to s^2 + 4s + 8.

Discrete time transfer functions are implemented by using the ‘dt’ class variable and setting it to something other than ‘None’. If ‘dt’ has a non-zero value, then it must match whenever two transfer functions are combined. If ‘dt’ is set to True, the system will be treated as a discrete time system with unspecified sampling time.

control.tf(*args)¶

Create a transfer function system. Can create MIMO systems.

The function accepts either 1 or 2 parameters:

tf(sys)

Convert a linear system into transfer function form. Always creates a new system, even if sys is already a TransferFunction object.

tf(num, den)

Create a transfer function system from its numerator and denominator polynomial coefficients.

If num and den are 1D array_like objects, the function creates a SISO system.

To create a MIMO system, num and den need to be 2D nested lists of array_like objects. (A 3 dimensional data structure in total.) (For details see note below.)

tf(num, den, dt)

Create a discrete time transfer function system; dt can either be a positive number indicating the sampling time or ‘True’ if no specific timebase is given.

Parameters:

sys: Lti (StateSpace or TransferFunction)

A linear system

num: array_like, or list of list of array_like

Polynomial coefficients of the numerator

den: array_like, or list of list of array_like

Polynomial coefficients of the denominator

Returns:

out: TransferFunction

The new linear system

Raises:

ValueError

if num and den have invalid or unequal dimensions

TypeError

if num or den are of incorrect type

See also

ss, ss2tf, tf2ss

Notes

Todo

The next paragraph contradicts the comment in the example! Also “input” should come before “output” in the sentence:

“from the (j+1)st output to the (i+1)st input”

num[i][j] contains the polynomial coefficients of the numerator for the transfer function from the (j+1)st output to the (i+1)st input. den[i][j] works the same way.

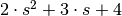The coefficients [2, 3, 4] denote the polynomial $2 \cdot s^2 + 3 \cdot s + 4$ .

Examples

>>> # Create a MIMO transfer function object
>>> # The transfer function from the 2nd input to the 1st output is
>>> # (3s + 4) / (6s^2 + 5s + 4).
>>> num = [[[1., 2.], [3., 4.]], [[5., 6.], [7., 8.]]]
>>> den = [[[9., 8., 7.], [6., 5., 4.]], [[3., 2., 1.], [-1., -2., -3.]]]
>>> sys1 = tf(num, den)

>>> # Convert a StateSpace to a TransferFunction object.
>>> sys_ss = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.")
>>> sys2 = tf(sys1) 

Utility functions and converstions¶

control.drss(states=1, outputs=1, inputs=1)¶

Create a stable discrete random state space object.

Parameters:

states: integer

Number of state variables

inputs: integer

Number of system inputs

outputs: integer

Number of system outputs

Returns:

sys: StateSpace

The randomly created linear system

Raises:

ValueError

if any input is not a positive integer

See also

rss

Notes

If the number of states, inputs, or outputs is not specified, then the missing numbers are assumed to be 1. The poles of the returned system will always have a magnitude less than 1.

control.isctime(sys, strict=False)¶

Check to see if a system is a continuous time system

Parameters:

sys : LTI system

System to be checked

strict: bool (default = False)

If strict is True, make sure that timebase is not None

control.isdtime(sys, strict=False)¶

Check to see if a system is a discrete time system

Parameters:

sys : LTI system

System to be checked

strict: bool (default = False)

If strict is True, make sure that timebase is not None

control.issys(object)¶

control.pade(T, n=1)¶

Create a linear system that approximates a delay.

Return the numerator and denominator coefficients of the Pade approximation.

Parameters:

T : number

time delay

n : integer

order of approximation

Returns:

num, den : array

Polynomial coefficients of the delay model, in descending powers of s.

Notes

Based on an algorithm in Golub and van Loan, “Matrix Computation” 3rd. Ed. pp. 572-574.

control.sample_system(sysc, Ts, method='matched')¶

Convert a continuous time system to discrete time

Creates a discrete time system from a continuous time system by sampling. Multiple methods of conversion are supported.

Parameters:

sysc : linsys

Continuous time system to be converted

Ts : real

Sampling period

method : string

Method to use for conversion: ‘matched’ (default), ‘tustin’, ‘zoh’

Returns:

sysd : linsys

Discrete time system, with sampling rate Ts

Notes

The conversion methods ‘tustin’ and ‘zoh’ require the cont2discrete() function, including in SciPy 0.10.0 and above.
Additional methods ‘foh’ and ‘impulse’ are planned for future implementation.

Examples

>>> sysc = TransferFunction([1], [1, 2, 1])
>>> sysd = sample_system(sysc, 1, method='matched')

control.ss2tf(*args)¶

Transform a state space system to a transfer function.

The function accepts either 1 or 4 parameters:

ss2tf(sys)

Convert a linear system into space system form. Always creates a new system, even if sys is already a StateSpace object.

ss2tf(A, B, C, D)

Create a state space system from the matrices of its state and output equations.

For details see: ss()

Parameters:

sys: StateSpace

A linear system

A: array_like or string

System matrix

B: array_like or string

Control matrix

C: array_like or string

Output matrix

D: array_like or string

Feed forward matrix

Returns:

out: TransferFunction

New linear system in transfer function form

Raises:

ValueError

if matrix sizes are not self-consistent, or if an invalid number of arguments is passed in

TypeError

if sys is not a StateSpace object

See also

tf, ss, tf2ss

Examples

>>> A = [[1., -2], [3, -4]]
>>> B = [[5.], [7]]
>>> C = [[6., 8]]
>>> D = [[9.]]
>>> sys1 = ss2tf(A, B, C, D)

>>> sys_ss = ss(A, B, C, D)
>>> sys2 = ss2tf(sys_ss) 

control.ssdata(sys)¶

Return state space data objects for a system

Parameters:

sys: Lti (StateSpace, or TransferFunction)

LTI system whose data will be returned

Returns:

(A, B, C, D): list of matrices

State space data for the system

control.tf2ss(*args)¶

Transform a transfer function to a state space system.

The function accepts either 1 or 2 parameters:

tf2ss(sys)

Convert a linear system into transfer function form. Always creates a new system, even if sys is already a TransferFunction object.

tf2ss(num, den)

Create a transfer function system from its numerator and denominator polynomial coefficients.

For details see: tf()

Parameters:

sys: Lti (StateSpace or TransferFunction)

A linear system

num: array_like, or list of list of array_like

Polynomial coefficients of the numerator

den: array_like, or list of list of array_like

Polynomial coefficients of the denominator

Returns:

out: StateSpace

New linear system in state space form

Raises:

ValueError

if num and den have invalid or unequal dimensions, or if an invalid number of arguments is passed in

TypeError

if num or den are of incorrect type, or if sys is not a TransferFunction object

See also

ss, tf, ss2tf

Examples

>>> num = [[[1., 2.], [3., 4.]], [[5., 6.], [7., 8.]]]
>>> den = [[[9., 8., 7.], [6., 5., 4.]], [[3., 2., 1.], [-1., -2., -3.]]]
>>> sys1 = tf2ss(num, den)

>>> sys_tf = tf(num, den)
>>> sys2 = tf2ss(sys_tf) 

control.tfdata(sys, **kw)¶

Return transfer function data objects for a system

Parameters:

sys: Lti (StateSpace, or TransferFunction)

LTI system whose data will be returned

Returns:

(num, den): numerator and denominator arrays

Transfer function coefficients (SISO only)

control.timebase(sys, strict=True)¶

Return the timebase for an Lti system

dt = timebase(sys)

returns the timebase for a system ‘sys’. If the strict option is set to False, dt = True will be returned as 1.

control.timebaseEqual(sys1, sys2)¶

Check to see if two systems have the same timebase

timebaseEqual(sys1, sys2)

returns True if the timebases for the two systems are compatible. By default, systems with timebase ‘None’ are compatible with either discrete or continuous timebase systems. If two systems have a discrete timebase (dt > 0) then their timebases must be equal.

Creating System Models¶

System creation¶

Utility functions and converstions¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

Creating System Models¶

System creation¶

Utility functions and converstions¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation