Control System Analysis

control.acker(A, B, poles)

Pole placement using Ackermann method

Call: K = acker(A, B, poles)

Parameters:

A, B : 2-d arrays

State and input matrix of the system

poles: 1-d list

Desired eigenvalue locations

Returns:

K: matrix

Gains such that A - B K has given eigenvalues

control.ctrb(A, B)

Controllabilty matrix

Parameters:

A, B: array_like or string

Dynamics and input matrix of the system

Returns:

C: matrix

Controllability matrix

Examples

>>> C = ctrb(A, B)

control.care(A, B, Q, R=None, S=None, E=None)

(X,L,G) = care(A,B,Q) solves the continuous-time algebraic Riccati equation

A^T X + X A - X B B^T X + Q = 0

where A and Q are square matrices of the same dimension. Further, Q is a symmetric matrix. The function returns the solution X, the gain matrix G = B^T X and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G.

(X,L,G) = care(A,B,Q,R,S,E) solves the generalized continuous-time algebraic Riccati equation

A^T X E + E^T X A - (E^T X B + S) R^-1 (B^T X E + S^T) + Q = 0

where A, Q and E are square matrices of the same dimension. Further, Q and R are symmetric matrices. The function returns the solution X, the gain matrix G = R^-1 (B^T X E + S^T) and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G , E.

control.dare(A, B, Q, R, S=None, E=None)

(X,L,G) = dare(A,B,Q,R) solves the discrete-time algebraic Riccati equation

A^T X A - X - A^T X B (B^T X B + R)^-1 B^T X A + Q = 0

where A and Q are square matrices of the same dimension. Further, Q is a symmetric matrix. The function returns the solution X, the gain matrix G = (B^T X B + R)^-1 B^T X A and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G.

(X,L,G) = dare(A,B,Q,R,S,E) solves the generalized discrete-time algebraic Riccati equation

A^T X A - E^T X E - (A^T X B + S) (B^T X B + R)^-1 (B^T X A + S^T) +

• Q = 0

where A, Q and E are square matrices of the same dimension. Further, Q and R are symmetric matrices. The function returns the solution X, the gain matrix G = (B^T X B + R)^-1 (B^T X A + S^T) and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G , E.

control.dlyap(A, Q, C=None, E=None)

dlyap(A,Q) solves the discrete-time Lyapunov equation

A X A^T - X + Q = 0

where A and Q are square matrices of the same dimension. Further Q must be symmetric.

dlyap(A,Q,C) solves the Sylvester equation

A X Q^T - X + C = 0

where A and Q are square matrices.

dlyap(A,Q,None,E) solves the generalized discrete-time Lyapunov equation

A X A^T - E X E^T + Q = 0

where Q is a symmetric matrix and A, Q and E are square matrices of the same dimension.

control.dcgain(*args)

Compute the gain of the system in steady state.

The function takes either 1, 2, 3, or 4 parameters:

Parameters:

A, B, C, D: array-like

A linear system in state space form.

Z, P, k: array-like, array-like, number

A linear system in zero, pole, gain form.

num, den: array-like

A linear system in transfer function form.

sys: Lti (StateSpace or TransferFunction)

A linear system object.

Returns:

gain: matrix

The gain of each output versus each input:

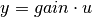
Notes

This function is only useful for systems with invertible system matrix A.

All systems are first converted to state space form. The function then computes:

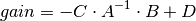
control.evalfr(sys, x)

Evaluate the transfer function of an LTI system for a single complex number x.

To evaluate at a frequency, enter x = omega*j, where omega is the frequency in radians

Parameters:

sys: StateSpace or TransferFunction

Linear system

x: scalar

Complex number

Returns:

fresp: ndarray

See also

freqresp, bode

Notes

This function is a wrapper for StateSpace.evalfr and TransferFunction.evalfr.

Examples

>>> sys = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.")
>>> evalfr(sys, 1j)
array([[ 44.8-21.4j]])
>>> # This is the transfer function matrix evaluated at s = i.

Todo

Add example with MIMO system

control.gram(sys, type)

Gramian (controllability or observability)

Parameters:

sys: StateSpace

State-space system to compute Gramian for

type: String

Type of desired computation. type is either ‘c’ (controllability) or ‘o’ (observability).

Returns:

gram: array

Gramian of system

Raises:

ValueError

• if system is not instance of StateSpace class
• if type is not ‘c’ or ‘o’
• if system is unstable (sys.A has eigenvalues not in left half plane)

ImportError

if slycot routin sb03md cannot be found

Examples

>>> Wc = gram(sys,'c')
>>> Wo = gram(sys,'o')

control.lyap(A, Q, C=None, E=None)

X = lyap(A,Q) solves the continuous-time Lyapunov equation

A X + X A^T + Q = 0

where A and Q are square matrices of the same dimension. Further, Q must be symmetric.

X = lyap(A,Q,C) solves the Sylvester equation

A X + X Q + C = 0

where A and Q are square matrices.

X = lyap(A,Q,None,E) solves the generalized continuous-time Lyapunov equation

A X E^T + E X A^T + Q = 0

where Q is a symmetric matrix and A, Q and E are square matrices of the same dimension.

control.freqresp(sys, omega)

Frequency response of an LTI system at multiple angular frequencies.

Parameters:

sys: StateSpace or TransferFunction

Linear system

omega: array_like

List of frequencies

Returns:

mag: ndarray

phase: ndarray

omega: list, tuple, or ndarray

See also

evalfr, bode

Notes

This function is a wrapper for StateSpace.freqresp and TransferFunction.freqresp. The output omega is a sorted version of the input omega.

Examples

>>> sys = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.")
>>> mag, phase, omega = freqresp(sys, [0.1, 1., 10.])
>>> mag
array([[[ 58.8576682 ,  49.64876635,  13.40825927]]])
>>> phase
array([[[-0.05408304, -0.44563154, -0.66837155]]])

Todo

Add example with MIMO system

#>>> sys = rss(3, 2, 2) #>>> mag, phase, omega = freqresp(sys, [0.1, 1., 10.]) #>>> mag[0, 1, :] #array([ 55.43747231, 42.47766549, 1.97225895]) #>>> phase[1, 0, :] #array([-0.12611087, -1.14294316, 2.5764547 ]) #>>> # This is the magnitude of the frequency response from the 2nd #>>> # input to the 1st output, and the phase (in radians) of the #>>> # frequency response from the 1st input to the 2nd output, for #>>> # s = 0.1i, i, 10i.

control.margin(*args)

Calculate gain and phase margins and associated crossover frequencies

Function margin takes either 1 or 3 parameters.

Parameters:

sys : StateSpace or TransferFunction

Linear SISO system

mag, phase, w : array_like

Input magnitude, phase (in deg.), and frequencies (rad/sec) from bode frequency response data

Returns:

gm, pm, Wcg, Wcp : float

Gain margin gm, phase margin pm (in deg), gain crossover frequency (corresponding to phase margin) and phase crossover frequency (corresponding to gain margin), in rad/sec of SISO open-loop. If more than one crossover frequency is detected, returns the lowest corresponding margin.

Examples

>>> sys = ss("1. -2; 3. -4", "5.; 7", "6. 8", "9.")
>>> gm, pm, wg, wp = margin(sys)
margin: no magnitude crossings found

Todo

better ecample system!

#>>> gm, pm, wg, wp = margin(mag, phase, w)

control.markov(Y, U, M)

Calculate the first M Markov parameters [D CB CAB ...] from input U, output Y.

Parameters:

Y: array_like

Output data

U: array_like

Input data

M: integer

Number of Markov parameters to output

Returns:

H: matrix

First M Markov parameters

Notes

Currently only works for SISO

Examples

>>> H = markov(Y, U, M)

control.obsv(A, C)

Observability matrix

Parameters:

A, C: array_like or string

Dynamics and output matrix of the system

Returns:

O: matrix

Observability matrix

Examples

>>> O = obsv(A, C)

control.phase_crossover_frequencies(sys)

Compute frequencies and gains at intersections with real axis in Nyquist plot.

Call as:

omega, gain = phase_crossover_frequencies()

Returns:

omega: 1d array of (non-negative) frequencies where Nyquist plot

intersects the real axis

gain: 1d array of corresponding gains

Examples

>>> tf = TransferFunction([1], [1, 2, 3, 4])
>>> PhaseCrossoverFrequenies(tf)
(array([ 1.73205081,  0.        ]), array([-0.5 ,  0.25]))

control.pole(sys)

Compute system poles.

Parameters:

sys: StateSpace or TransferFunction

Linear system

Returns:

poles: ndarray

Array that contains the system’s poles.

Raises:

NotImplementedError

when called on a TransferFunction object

See also

zero

Notes

This function is a wrapper for StateSpace.pole and TransferFunction.pole.

control.root_locus(sys, kvect, xlim=None, ylim=None, plotstr='-', Plot=True, PrintGain=True)

Calculate the root locus by finding the roots of 1+k*TF(s) where TF is self.num(s)/self.den(s) and each k is an element of kvect.

Parameters:

sys : linsys

Linear input/output systems (SISO only, for now)

kvect : gain_range (default = None)

List of gains to use in computing diagram

Plot : boolean (default = True)

If True, plot magnitude and phase

PrintGain: boolean (default = True)

If True, report mouse clicks when close to the root-locus branches, calculate gain, damping and print

Return values

————-

rlist : list of computed root locations

control.stability_margins(sysdata, deg=True, returnall=False, epsw=1e-12)

Calculate gain, phase and stability margins and associated crossover frequencies.

Parameters:

sysdata: linsys or (mag, phase, omega) sequence

sys : linsys

Linear SISO system

mag, phase, omega : sequence of array_like

Input magnitude, phase, and frequencies (rad/sec) sequence from bode frequency response data

deg=True: boolean

If true, all input and output phases in degrees, else in radians

returnall=False: boolean

If true, return all margins found. Note that for frequency data or FRD systems, only one margin is found and returned.

epsw=1e-12: float

frequencies below this value are considered static gain, and not returned as margin.

Returns:

gm, pm, sm, wg, wp, ws: float or array_like

Gain margin gm, phase margin pm, stability margin sm, and associated crossover frequencies wg, wp, and ws of SISO open-loop. If more than one crossover frequency is detected, returns the lowest corresponding margin. When requesting all margins, the return values are array_like, and all margins are returns for linear systems not equal to FRD

control.zero(sys)

Compute system zeros.

Parameters:

sys: StateSpace or TransferFunction

Linear system

Returns:

zeros: ndarray

Array that contains the system’s zeros.

Raises:

NotImplementedError

when called on a TransferFunction object or a MIMO StateSpace object

See also

pole

Notes

This function is a wrapper for StateSpace.zero and TransferFunction.zero.